Regresji Excel: przykłady równanie. regresji liniowej

Analiza regresji – statystyczny metoda badania, aby pokazać zależność parametru jednego lub więcej niezależnych zmiennych. W epoce przed komputerem, jego zastosowanie jest dość trudne, zwłaszcza gdy doszło do dużych ilości danych. Dzisiaj, uczenie się, jak zbudować regresji w programie Excel, można rozwiązać złożone problemy statystyczne w ciągu zaledwie kilku minut. Poniżej przedstawiono konkretne przykłady ekonomii.

rodzaje regresji

Pojęcie to zostało wprowadzone do matematyki przez Francisa Galtona w 1886 roku. Regresja jest:

• liniowy;
• paraboliczne;
• moc;
• wykładniczy;
• hiperboliczny;
• wykładniczy;
• logarytmiczna.

Przykład 1

Rozważ problem określenia zależność liczby rezygnacji członków personelu średniego wynagrodzenia w 6 przedsiębiorstwach przemysłowych.

Zadaniem. Sześć firm Zbadaliśmy przeciętnego miesięcznego wynagrodzenia i liczby pracowników, którzy rzucili się dobrowolnie. W formie tabelarycznej mamy:

W przypadku problemu określania zależności pracowników ilość separacje od średniej wynagrodzenia 6 przedsiębiorstw modelu regresji ma postać równania: y = A ₀ + a ₁ x ₁ + … + _K x _K, gdzie x _i – zmienne mające wpływ, _I – współczynniki regresji ak – szereg czynników.

Y dla danego zadania – jest to wskaźnik, aby zwolnić pracownika, czynnikiem – pensja, która jest oznaczona przez X.

Wykorzystanie mocy „Excel” arkusza kalkulacyjnego

Analiza regresji w programie Excel powinny być poprzedzone wnioskiem do istniejących danych tabeli wbudowanych funkcji. Jednak dla tych celów lepiej jest użyć bardzo użyteczny dodatek „analizy pakietów”. Aby go włączyć, trzeba:

• z zakładki „Plik” Idź do „Ustawienia”;
• W oknie, które zostanie otwarte, wybierz „Dodatki”;
• kliknąć na przycisk „GO”, znajdujący się w prawym dolnym rogu wierszu „zarządzania”;
• postawić znak wyboru obok „Analysis ToolPak” i potwierdź działanie, naciskając „OK”.

Jeśli wykonane prawidłowo, po prawej stronie zakładki „Dane”, znajduje się nad arkuszem roboczym „Excel”, przedstawia odpowiedni przycisk.

Regresji liniowej w Excelu

Teraz, że masz pod ręką wszystkie niezbędne narzędzia wirtualne dla obliczeń ekonometrycznych, możemy zacząć rozwiązać nasz problem. Aby to zrobić:

• kliknięciu przycisku na „Analiza danych”;
• kliknij na przycisk „regresja” w otwartym oknie;
• języczek, który wydaje się wprowadzenie szeregu wartości Y (liczby rozdzieleń pracowników) i X (wynagrodzenia);
• potwierdzają swoje działania poprzez naciśnięcie przycisku «OK».

W rezultacie, program automatycznie wypełni nową analizę regresji danych arkusza kalkulacyjnego. Zwrócić uwagę! W programie Excel, istnieje możliwość, aby ustawić miejsce, które wolisz do tego celu. Na przykład, może to być ten sam arkusz, gdzie wartości X i Y, a nawet nowa książka, zaprojektowany specjalnie do przechowywania takich danych.

Wyniki analizy regresji dla R-kwadrat

Dane uzyskane w Excel rozważanych przykład dane mają postać:

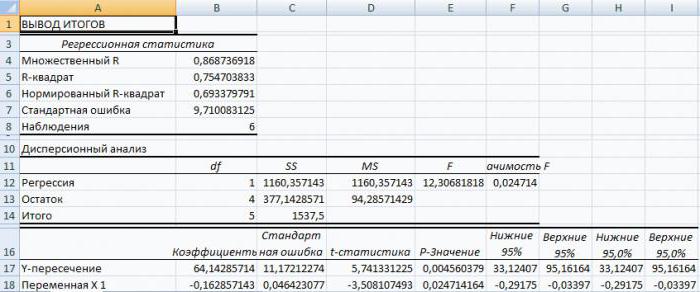
Przede wszystkim należy zwrócić uwagę na wartość R-kwadrat. Reprezentuje współczynnik korelacji. W tym przykładzie, R-kwadrat = 0,755 (75,5%), m. E. obliczone parametry modelu, aby wyjaśnić związek pomiędzy parametrów rozważanych przez 75,5%. Im wyższa wartość współczynnika określenia wybrany model jest uważane za bardziej użyteczne dla poszczególnych zadań. Uważa się, że prawidłowo opisują faktycznej sytuacji na wartość R-kwadrat powyżej 0,8. Jeśli R-kwadrat <0,5, a następnie przeprowadzono analizę regresji Excel nie można uznać za uzasadnione.

analiza stosunek

Ilość 64,1428 pokazuje, jaka będzie wartość Y, jeśli wszystkie zmienne xi w naszym modelu zostaną zresetowane. Innymi słowy, można stwierdzić, że wartość analizowanego parametru jest pod wpływem innych czynników, niż te opisane w konkretnym modelu.

Kolejnym czynnikiem -0,16285 się w B18 komórek przedstawia istotny wpływ zmiennej X, Y. Oznacza to, że średnie zarobki pracowników w modelu wpływa na liczbę rezygnacji z ciężaru -0.16285, t. E. stopnia jego oddziaływania na cały mała. Znak „-” oznacza, że współczynnik jest ujemny. Jest to oczywiste, ponieważ wszyscy wiemy, że im bardziej płaca w przedsiębiorstwie, tym mniej osób wyraziło chęć wypowiedzenia umowy o pracę lub odrzucić.

regresji wielokrotnej

Pod pojęcie to odnosi się do równania komunikacji z kilku niezależnych zmiennych, o postaci:

y = f (x ₁ + x ₂ + … _Xm) + ε, gdzie R – stanowi wynik funkcja (zmienna zależna), a X _{1, X2 … Xm} – są znaki czynniki (zmienne niezależne).

estymacja parametrów

Do regresji wielokrotnej (MR) jest przeprowadzana przy użyciu metody najmniejszych kwadratów (LSM). Równań liniowych o postaci y = a + b ₁ x _{1 + … + B m x m +} ε budowę systemu równań normalnych (cm. Poniżej)

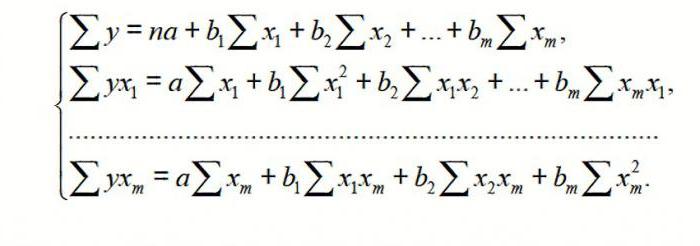
Aby zrozumieć zasadę metody, rozważymy przypadek dwuskładnikowego. Następnie mamy sytuacja opisana za pomocą wzoru

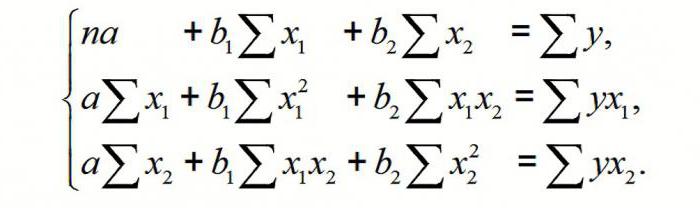
Stąd otrzymujemy:

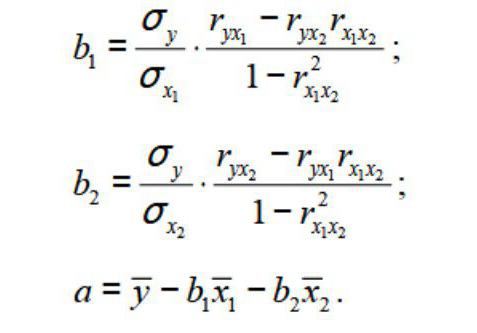
gdzie σ – wariancja jest odpowiedniej funkcji, odzwierciedlone w indeksie.

MNC ma zastosowanie do równania MR do standartiziruemom skalę. W tym przypadku otrzymujemy równanie:

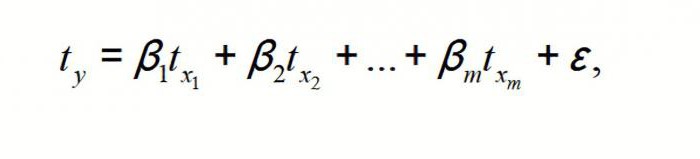
znamienny t _{y t x 1, …,} T _xm – standartiziruemye zmiennych dla której średnie wartości 0; p _i – znormalizowanych współczynników regresji i odchylenie standardowe – 1.

Należy pamiętać, że wszystkie p _I w tym przypadku określana jako znormalizowana i tsentraliziruemye zatem porównania pomiędzy uważane za ważne i akceptowalne. Ponadto przyjmuje się, do przeprowadzenia badań przesiewowych czynników, odrzucając te, które mają najniższe wartości βi.

Problem z wykorzystaniem równania regresji liniowej

Załóżmy, że masz stolik dynamiki cen danego produktu N w ciągu ostatnich 8 miesięcy. Konieczne jest, aby zdecydować, czy nabycie jego partii w cenie 1850 rubli. / T.

Aby rozwiązać ten problem w tabelarycznej procesora „Excel” wymagane do korzystania już znane na przykład narzędzia „Analiza danych” przedstawionej powyżej. Następnie należy wybrać sekcję „regresja” i ustaw parametry. Musimy pamiętać, że w „zasięgu wejściowy Y» powinny zostać wprowadzone do zakresu wartości zmiennej zależnej (w tym przypadku ceny towarów w poszczególnych miesiącach roku) oraz w „Input przedział X» – za niezależną (miesiąc). Potwierdzamy akcję klikając «OK». W nowym arkuszu (jeśli tak podane), otrzymujemy dane dla regresji.

Jesteśmy w oparciu o ich liniowe równanie postaci y = ax + b, gdzie jak a parametry a i b są współczynnikami z numerem linii miesiąca i nazwa współczynników i «„linii Y przecięcia arkusza z wynikami analizy regresji. Tak więc, równania regresji liniowej (EQ) 3 do problemu może być zapisana jako:

Cena towaru N = numer 11714 * 1727,54 miesięcy +.

lub w notacji algebraicznej

T = x + 11714 1727,54

Analiza wyników

Aby zdecydować, czy odebrany odpowiednio liniowego równania regresji przy użyciu wielu współczynników korelacji (CMC) i określenie, jak również jako test i t-testu Fishera. W tabeli „Excel” regresji z wynikami działają one pod nazwami wielokrotność R, R-kwadrat, F-t-statystyk i, odpowiednio.

KMC R umożliwia oszacowanie bliskości probabilistyczny zależność pomiędzy zmiennych niezależnych i zależnych. Jego wysoka wartość wskazuje na dość silny związek między zmienną „numer miesiąca” i „N Cena produktu w rubli za 1 tonę.” Jednak charakter tej relacji nie jest znana.

Kwadrat współczynnika określania ^R2 (RI) jest numeryczny charakterystyczne proporcji całkowitego rozproszenia i wykazuje rozrzut eksperymentalnej części danych, to znaczy wartości zmiennej zależnej odpowiadającej równania regresji liniowej. W ten problem, wartość ta jest 84,8%, temperatura topnienia. E. Statystyki z wysokim stopniem dokładności uzyskanej opisano SD.

F statystyki, znane również jako kryterium Fishera zastosowano do oceny istotności zależność liniową lub podważania hipotezę, potwierdzając jego istnienie.

Wartość statystyki t (test t Studenta) pomaga ocenić znaczenie współczynnika w każdej wolnej nieznanego członka liniowej zależności. Jeżeli wartość testu t> t _{cr hipoteza} liniowego równania nieistotności wolnej termin jest odrzucany.

W tym problem dla wolnego terminu poprzez instrumenty „Excel” stwierdzono, że t = 169,20903, oraz p = 2,89E-12, t. E. Mają prawdopodobieństwo zerowe, że wierni będą odrzucił hipotezę o nieistotności wolnego terminu. Nieznanych współczynnikiem w czasie t = 5,79405, a P = 0,001158. Innymi słowy, prawdopodobieństwo, że zostanie odrzucona hipoteza poprawne znikomości współczynnika dla nieznanego, wynosi 0,12%.

Tak więc, można stwierdzić, że uzyskano równanie regresji liniowej odpowiednio.

Problem celowości zakupu akcji

Regresji wielokrotnej przeprowadzono w programie Excel przy użyciu tej samej funkcji „analiza danych”. Rozważmy konkretną aplikację.

Przewodnik firma «NNN» musi zdecydować, czy do zakupu 20% akcji JSC «MMM». Cena pakietu (SP) jest 70 milionów dolarów. Specjaliści «» NNN zebrano dane na temat podobnych transakcji. Zdecydowano, aby ocenić wartość udziałów o takich parametrach, wyrażony w milionach dolarów amerykańskich, takich jak:

• zobowiązania (VK);
• Wielkość rocznego obrotu (VO);
• należności (Vd);
• Wartość trwałych (SOF).

Ponadto, korzystając z długów płac przedsiębiorstw (V3 u) w tysiącach dolarów amerykańskich.

Procesor stół decyzja środki Excel

Najpierw trzeba utworzyć tabelę danych wejściowych. Jest to w następujący sposób:

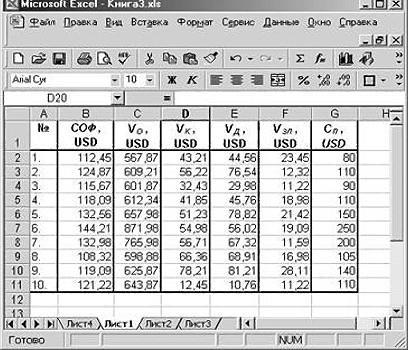
Dalej:

• call box "analiza danych";
• Wybrany fragment „regresja”;
• „okno wejściowe przedział Y» podawany zakres zależne zmienne wartości z kolumny G;
• kliknij na ikonę z czerwoną strzałką po prawej stronie okna „Wejście przedział X» i samodzielnie na zakresu arkusza wszystkich wartości kolumny B, C, D, F.

Zaznaczyć punkt „Nowy arkusz” i kliknij „OK”.

Dostać analizę regresji dla tego zadania.

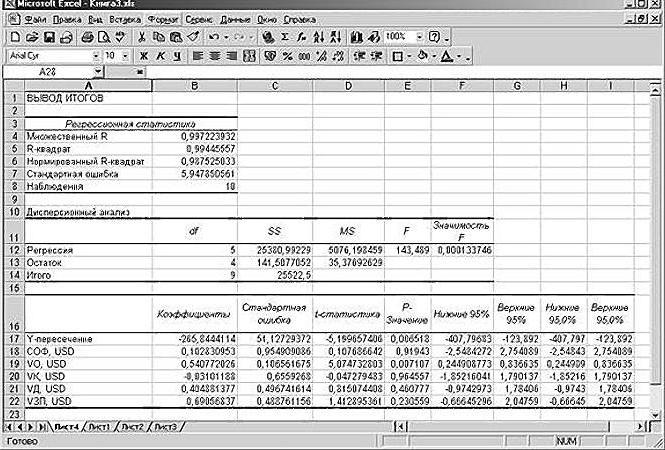
Wyniki badań i wnioski

„Zbierać” zaokrąglone z danych przedstawionych powyżej w równaniu Excel regresji procesor tabeli arkusza:

SD = 0,103 * SOF + 0541 * VO – 0031 * VK + 0405 + 0691 * VD * VZP – 265.844.

W bardziej zwykłej postaci matematycznej można zapisać jako:

Y = 0103 * 0541 * x1 + x2 – 0,031 * 0,405 * x3 + x4 + 0691 * x5 – 265.844

Dane dla «MMM» JSC przedstawione w poniższej tabeli:

Podstawiając je do równania regresji, uzyskał postać 64.72 milionów dolarów. Oznacza to, że akcje JSC «» MMM nie należy kupować, ponieważ ich koszt jest dość drogie na 70 milionów dolarów.

Jak widać, wykorzystanie arkusza kalkulacyjnego „Excel” i równanie regresji mogą podjąć świadomą decyzję dotyczącą celowości całkiem konkretną transakcję.

Teraz już wiesz, co to regresja. Przykłady do Excela, omówione powyżej, pomoże Ci w rozwiązywaniu praktycznych problemów ekonometrii.