Równolegle do płaszczyzny: stan i właściwości

Równolegle do płaszczyzny jest pojęciem pierwszy pojawił się w geometrii euklidesowej przez ponad dwa tysiące lat temu.

Główne cechy geometrii klasycznej

Narodziny tej dyscypliny naukowej związanej ze znanych dzieł starożytnego greckiego filozofa Euklidesa, który napisał w trzecim wieku przed naszą erą, broszurze „Elements”. Podzielone na trzynaście książek, „Elements” jest najwyższym osiągnięciem wszystkich starożytnych matematyki i wyłożył podstawowe założenia związane z właściwościami figur płaskich.

Stan klasyczny równoległych płaszczyznach sformułowano w sposób następujący: dwie płaszczyzny mogą być nazywane równoległe, jeśli każde z nich nie mają wspólnych punktów. Czytaj euklidesową piąty postulat pracy.

Właściwości równoległych płaszczyznach

Geometria euklidesowa pojedyncze, zwykle pięć:

• Obiekt jest pierwszym (i opisuje się równolegle do płaszczyzny ich niepowtarzalność). Za pośrednictwem jednego punktu, który znajduje się na zewnątrz tego konkretnego samolotu, możemy wyciągnąć jedną i tylko jedną płaszczyznę równoległą

• Druga właściwość (znany również jako właściwości trzech powtórzeniach). W przypadku, gdy dwie płaszczyzny są równoległe w stosunku do jednej trzeciej, od siebie, są także równoległe.

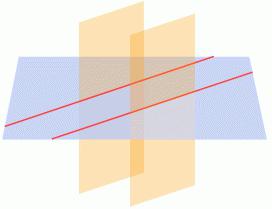
• Trzecia nieruchomość (innymi słowy, to się nazywa linię przecinającą nieruchomości równolegle do płaszczyzny). Jeśli potraktować oddzielnie linia prosta przecina jedną z tych równoległych płaszczyznach, to krzyż i drugiego.

• Obiekt czwarta (własność prostych wyryte w płaszczyznach równoległych do siebie). Gdy dwie równoległe płaszczyzny przecinają się trzecia (z każdej strony), oraz ich linii przecięcia są równoległe

• Właściwość piąta (właściwość, która opisuje różne segmenty równoległych prostych linii, które znajdują się między płaszczyznami równoległymi do siebie). Segmenty równoległych linii, które są zamknięte pomiędzy dwoma równoległymi płaszczyznami koniecznie równe.

Równolegle do płaszczyzny w geometrii nieeuklidesowej

Takie rozwiązanie jest w szczególności geometria Lobachevsky i Riemanna. Jeżeli geometria euklidesowa jest realizowany na płaskiej przestrzeni, następnie w Lobachevsky ujemnie zakrzywionych przestrzeniach (zakrzywione po prostu umieścić), natomiast Riemanna znajdzie swoją realizację w korzystnie zakrzywionych przestrzeniach (innymi słowy – obszary). Jest to bardzo powszechny pogląd, że stereotypowy Lobachevsky równolegle do płaszczyzny (a także linii) przecinają. 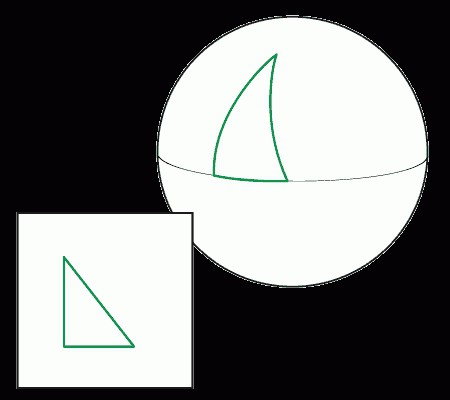Jednak nie jest to prawdą. Rzeczywiście narodziny geometrii hiperbolicznej wiązało się z dowodem piątego postulatu i zmieniając poglądy na niej Euklidesa, ale sama definicja równoległych płaszczyzn i prostych oznacza, że nie mogą one przekroczyć ani Lobachevsky ani Riemann, niezależnie od miejsca ich wprowadzeniem. Zmiana serca i treść jest następująca. Zamiast postulatem, że tylko jedna równoległa płaszczyzna może być wykorzystana przez punkt nie na danej płaszczyźnie, był inny preparat: Do punktu, który nie znajduje się na tym szczególnym płaszczyźnie może mieć dwie, co najmniej prostego, które znajdują się w jeden samolot z tym i nie przekroczyć.