Diagram Eulera: przykłady i możliwości

Matematyka jest zasadniczo streszczenie nauki, jeśli odejście od podstawowych pojęć. Tak więc, parę potrójnych jabłek można graficznie przedstawiają podstawowe operacje, które są podstawą matematyki, ale jak tylko płaszczyzna działalności rozszerza te obiekty nie wystarczy. Ktoś próbował przedstawiać na operacjach jabłka na nieskończonych zestawów? Fakt sprawy jest to, że nie. Im bardziej złożone koncepcje, która działa matematyki w swoim wyroku, tym bardziej problematyczne wydawało swój wizualny wyraz, który będzie zaprojektowany w celu ułatwienia zrozumienia. Jednak w szczęściu, jako nowoczesnych studentów i nauki w ogóle, zostały wycofane po Eulera, przykłady i możliwości, które omówimy poniżej.

Trochę historii

17 kwietnia 1707 dał światu nauki Leonarda Eylera – wybitny naukowiec, którego wkład do matematyki, fizyki, budownictwa okrętowego, a nawet teorii muzyki nie do przecenienia. Jego prace są rozpoznawane i popytu do dziś na całym świecie, pomimo faktu, że nauka nie stoi w miejscu. Szczególnie zabawne jest to, że Pan Euler był bezpośrednio zaangażowany w rozwój rosyjskiej szkoły wyższej matematyki, tym bardziej, że z woli losu, że dwa razy wróciliśmy do naszego państwa. Naukowiec miał wyjątkową zdolność do budowania przejrzysty w swoich algorytmów logicznych, odcinając wszystkie niepotrzebne i w żadnym momencie ruchomego od ogółu do specyficznych. Nie będziemy wyliczać wszystkie swoje zalety, jak to zajmie znaczną ilość czasu, i powróćmy do tematu artykułu. To on zasugerował użycie graficznej reprezentacji operacji na zbiorach. Diagram Eulera rozwiązanie do każdego, nawet najbardziej trudne zadania przygotowane, w stanie przedstawić wizualnie.

Co jest istotą?

W praktyce, po Euler schemat jest pokazany poniżej mogą być wykorzystywane nie tylko w matematyce, jak pojęcie „paczkach” nie są unikalne dla tej dyscypliny. Tak, zostały one z powodzeniem stosowane w zarządzaniu.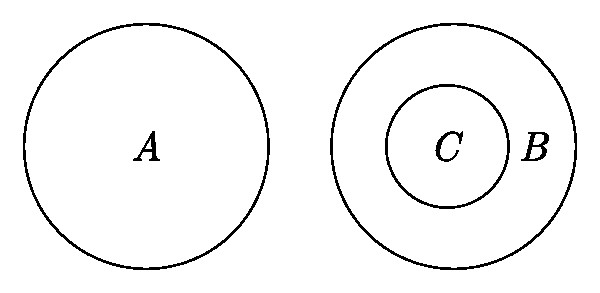

Schemat pokazuje powyższy związek ustawia (numer nieracjonalne), B (racjonalne liczby całkowite) oraz C (numery fizyczne). Okręgi wskazują, że zbiór jest zawarty w zbiorze B, to zbiór A nie przecinają się z nimi. Przykładem prostego, ale wyraźnie wyjaśnia specyfikę relacji „zestawów”, które są zbyt abstrakcyjne dla prawdziwego stosunku choćby dlatego ich nieskończoności.

algebra logiki

Ten obszar logiki matematycznej działa oświadczenia, które może być zarówno prawdziwe i fałszywe charakter. Na przykład, od elementarnych: liczba 625 jest podzielna przez 25, liczba 625 jest podzielna przez 5, liczba 625 jest prosta. Pierwszy i drugi zatwierdzenie – prawda, a drugi – to kłamstwo. Oczywiście, w praktyce jest to trudniejsze, ale punkt jest pokazany wyraźnie. I, oczywiście, decyzja ponownie zaangażowany schemat Eulera, przykłady ich użycia jest zbyt wygodny i intuicyjny, aby je zignorować.

Trochę teorii:

• Niech zestawu A i B występują i nie jest pusta, a następnie przez działanie przecięcia są następujące określone Association i negacji.
• Przecięcie zestawów A i B składa się z elementów, które należą do tego samego czasu ustawionego i ustalić B.
• Kombinacje A i B składa się z elementów, które należą do zestawu A lub B. zestaw
• Negacją zestawu – zestaw, który składa się z elementów, które nie należą do zbioru A.

Wszystko to ponownie przedstawiana jako Diagram Eulera w logice, jak z nimi każdego zadania, niezależnie od stopnia trudności staje się oczywiste i widoczne.

Aksjomaty algebry logiki

Załóżmy, że 1 i 0 są zdefiniowane i występują w rozmaitych A, a następnie:

• Negacją negacji zbioru jest zbiór A;
• Wiele łączności z ne_A oznacza 1;
• Wiele Związku 1 oznacza 1;
• Złącze zestawu z samym sobą jest zbiór A;
• Stowarzyszenie A 0 jest zbiór A;
• Wiele przecięcia z ne_A oznacza 0;
• Wiele przecięcia z siebie jest zestaw A;
• Przecięcie 0 to 0;
• Przecięcie 1 jest ustawiony A.

Główne własności algebry logiki

Niech zbiory A i B istnieją i nie są puste, a następnie:

• na skrzyżowaniu i unii zbiory A i B działa prawo przemienności;
• na skrzyżowaniu i unii zbiory A i B działa prawa łączności;
• na skrzyżowaniu i unii zbiory A i B działa prawo rozdzielcze;
• odmowa przecięcia A i B, to punkt przecięcia negacji A i B;
• negacja związek zestawów A i B jest sumą negacji A i B.

Poniżej przedstawiono następujące przykłady przecięcia Eulera łącząc zestawy A, B i C.

perspektywy

Prace Leonarda Eylera słusznie uważane za podstawę współczesnej matematyki, ale teraz są one z powodzeniem stosowane w dziedzinach działalności ludzkiej, które są stosunkowo nowe, do podjęcia co najmniej ładu korporacyjnego: Diagram Eulera, przykłady i wykresy opisują mechanizmy modeli rozwoju, zarówno w wersji rosyjskiej lub anglo-amerykańskiej ,