Przekątna trapezu równoboczny. Co jest w środku linii trapezu. Rodzaje trapezów. Trapez

Trapez – specjalny przypadek czworoboku, w którym jedna para boków jest równoległy. Określenie „trapez” pochodzi od greckiego słowa τράπεζα, czyli „stół”, „stół”. W tym artykule zajmiemy się rodzajami trapezu i jego właściwości. Ponadto przyjrzymy się, jak obliczyć poszczególne elementy figury geometrycznej. Na przykład, przekątna trapezu równobocznego, środkowej linii, powierzchni i innych. Materiał zawarty w geometrii elementarnej popularnego stylu, t. E. W łatwo dostępnym sposobem.

Przegląd

Najpierw zrozumieć, co czworobok. Liczba ta jest szczególnym przypadkiem wielokąta mającego cztery boki i cztery wierzchołki. Dwa wierzchołki czworokąta, które nie sąsiadują ze sobą, zwanych przeciwnie. To samo można powiedzieć o dwóch nie sąsiadujących ze sobą boków. Główne rodzaje czworokątów – równoległobok, prostokąt, romb, kwadrat, trapez i naramienny.

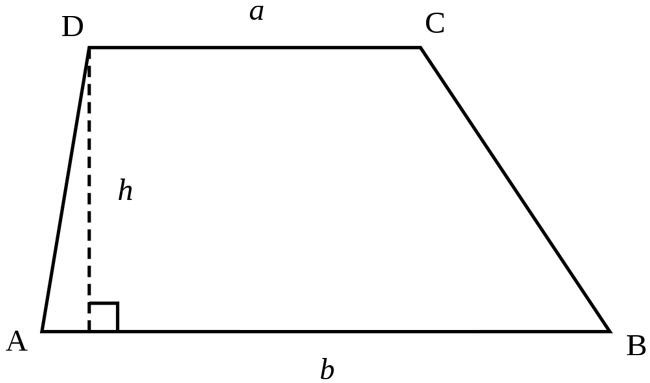
Keystone jest

Więc z powrotem do trapezu. Jak już powiedziano, figura dwa boki są równoległe. Nazywane są zasady. Dwa inne (nie-równoległy) – boki. Materiały z różnych badań i badań bardzo często można spotkać się wyzwań związanych z trapezów, których rozwiązanie wymaga często wiedzy studenta nie objętych programem. Szkoła geometria Kurs wprowadza uczniów z własności kątów i przekątnych, jak również linii środkowej trapezu równoramiennego. Ale inny niż wymieniony geometryczny kształt ma inne możliwości. Ale o nich później …

typy trapez

Istnieje wiele rodzajów tego rysunku. Jednak najczęściej w zwyczaju rozważać dwa z nich – równoramienny i prostokątny.

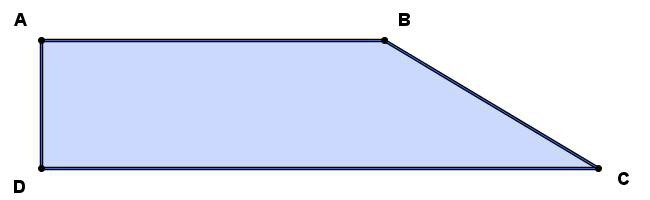
1. prostokątny trapez – postać, w której jeden z boków prostopadłych do podstawy. Ona ma dwa kąty są zawsze równa dziewięćdziesięciu stopni.

2. trapezu równoramiennego, – figura geometryczna, którego boki są równe. Tak, a kąty przy podstawie są również równe.

trapezowe z kątami prostymi

Główne zasady metod do badania właściwości trapezu

Podstawowe zasady obejmują stosowanie tzw podejścia zadaniowego. W rzeczywistości, nie ma potrzeby, aby wejść do teoretycznego kursu geometrii nowych właściwości tego rysunku. Mogą one być otwarte lub w procesie formułowania różnych zadań (lepszy system). Bardzo ważne jest, że nauczyciel wiedzieć, jakie zadania trzeba stawiać przed uczniami w danym momencie procesu uczenia się. Ponadto, każda nieruchomość trapez można przedstawić jako głównego zadania w systemie zadaniowego.

Drugą zasadą jest tzw organizacja spirala Badanie „niezwykłych” właściwości trapezie. Oznacza to powrót do procesu uczenia się do indywidualnych cech figury geometrycznej. W ten sposób uczniowie łatwiej je zapamiętać. Na przykład, obiekt z czterema punktami. można wykazać, jak w przypadku badań podobieństwa i następnie przy użyciu wektorów. Równomolowej trójkąty przylegające do boków na rysunku, można wykazać za pomocą nie tylko właściwości trójkąty równe wysokości przeprowadzonych na bokach, które znajdują się w linii prostej, ale także za pomocą wzorze S = 1/2 (ab * sinα). Ponadto, możliwe jest wypracowanie na twierdzenie sinusów do wpisanego trapezu lub trójkąta prostokątnego trapezu i opisanej w t. D.

Użycie „pozalekcyjnych” znajduje się geometryczny rysunek w treści kursu szkolnego – wielozadaniowych ich technologii nauczania. Stałe odniesienie do badania właściwości z upływem drugiej pozwala studentom nauczyć się trapez głębiej i zapewnia powodzenie zadania. Więc przystępujemy do badania tej niezwykłej postaci.

suma kątów trapezu równoramiennego

Elementy i właściwości równoramiennego trapezu

Jak już wspomniano, w tej figury geometrycznej boków są równe. Mimo to znane jest jako prawo trapezu. A co to jest tak niezwykłe i czemu zawdzięcza swoją nazwę? Szczególne cechy tej figury dotyczy, że ma nie tylko równe boki i kąty przy podstawie, ale również po przekątnej. Ponadto, suma kątów trapezu równoramiennego jest równy 360 stopni. Ale to nie wszystko! Tylko około równoramienny można opisać okrąg o wszystkich znanych trapezów. Jest to spowodowane tym, że suma kątów przeciwległe na tej figurze jest 180 stopni, a jedynie pod tym warunkiem można określić jako okrąg wokół czworoboku. Następujące właściwości z figury geometrycznej, że odległość od szczytu do podstawy w rzucie przeciwległych grzbietów na linii, który zawiera bazowy równa środkowej.

Teraz przyjrzyjmy się, jak znaleźć rogi trapezu równoramiennego. Rozważyć rozwiązanie tego problemu, pod warunkiem, że wielkość partii znana postać.

decyzja

Zwyczajowo oznaczają litery czworokąt A, B, C, D, gdzie BS i BP – fundament. W trapezu równoramiennego boki są równe. Zakładamy, że ich wielkość jest równa X i Y mają wymiary podstawy i Z (mniejsze i większe, odpowiednio). Do obliczenia kąta konieczności spędzają w wysokości H. Rezultatem jest trójkątem prostokątnym ABN gdzie AB – przeciwprostokątna i BN oraz – nogi. Obliczyć wielkość nogi AN: odejmowanie większej podstawy minimalnym, a wynik dzieli się przez 2 zapisu wzór: (ZY) / 2 = F. A teraz, w celu obliczenia kąta ostrego cos zastosowaniu w trójkąt. Otrzymuje się następujące dane: cos (β) = X / F Teraz obliczyć kąt: β arcos = (X / F). Ponadto, wiedząc, jeden róg, możemy określić, a po drugie, aby dokonać tej elementarnej arytmetyki operacji: 180 – p. Wszystkie kąty są zdefiniowane.

Jest też drugie rozwiązanie tego problemu. Na początku jest pominięte w rogu na wysokości nóg N. oblicza wartość BN. Wiemy, że kwadrat przeciwprostokątnej trójkąta prostokątnego jest równa sumie kwadratów dwóch pozostałych boków. Dostajemy: BN = √ (X2 F2). Następnie używamy funkcji trygonometrycznych Tg. Wynikiem jest: β = arctg (BN / F). Kąt ostry znajduje. Następnie określamy kąt rozwarty jak w pierwszej metodzie.

Własność przekątnych trapezu równoramiennego

Najpierw piszemy czterech zasad. Jeżeli po przekątnej do trapezu równoramiennego są prostopadłe, a następnie:

– wysokość rysunku jest równa sumie zasad, podzielonej przez dwa;

– jego wysokość i środkowa linia są równe;

– powierzchnia trapezu jest równa kwadratu wysokości (linii środkowej pół zasad);

– kwadrat przekątnej kwadratu jest równa połowie sumę dwukrotnego kwadratowych zasad lub środkowej (wysokość).

Spójrzmy teraz na formuły definiującej przekątnej równoboczny trapezu. Ta informacja może być podzielony na cztery części:

1. Wzór Przekątna przez jej bok.

Zakładamy, że A jest – dolną podstawę, b – Najlepiej, C – równe boki, D – po przekątnej. W tym przypadku, długość może być określona w następujący sposób:

D = √ (C2 + A * B).

2. Wzór na przekątnej długości cosinus.

Zakładamy, że A oznacza – dolną podstawę, b – Najlepiej, C – równe boki, D – po przekątnej, a (na dolnym poziomie) i beta (górna zasada) – trapezowe narożach. Otrzymamy następujący wzór, na podstawie którego można obliczyć długości przekątnej:

– D = √ (A2 + S2-2A * C * cosα);

– D = √ (A2 + S2-2A * C * cosβ);

– D = √ (B2 + S2-2V * C * cosβ);

– D = √ (B2 + S2-2V * C * cosα).

3. Wzór Przekątna równoramiennego trapezu.

Zakładamy, że A jest – dolna podstawa B – górna, D – po przekątnej, M – linia środkowa H – wysokość P – powierzchnia trapezu, a i β – kąt pomiędzy przekątnymi. Określić długość poniższych wzorów:

– D = √ (m2 + N2);

– D = √ (H2 + (A + B), 2/4);

– D = √ (N (A + B) / sinα) = √ (2n / sinα) = √ (2 M * N- / sinα).

W tym przypadku, równość: sinα = sinβ.

4. Wzór długości poprzez ukośne boki i wysokości.

Zakładamy, że A oznacza – dolną podstawę, b – Najlepiej, C – ściany, przekątnej D – H – wysokość, α – kąt z dolnej podstawy.

Określić długość poniższych wzorów:

– D = √ (H2 + (A-P * ctgα) 2);

– D = √ (H 2 + (B + C ctgα *) 2);

– D = √ (A2 + S2-2A * √ (C2-H2)).

przekątna trapezu równobocznego

Elementy i właściwości prostokątnego trapezu

Spójrzmy na to, co jest zainteresowany tą figurą geometryczną. Jak już powiedzieliśmy, możemy mieć prostokątny trapez dwa kąty proste.

Oprócz klasycznej definicji, są inni. Na przykład, prostokątny trapez – trapezoid, w którym z jednej strony jest prostopadły do podstawy. Lub kształt mający co kątów bocznych. W tego typu wysokości trapezów jest ta strona, która jest prostopadła do podstawy. Środkowa linia – odcinek łączący punkty środkowe obu stronach. Właściwość tego elementu jest to, że równolegle do podstawy i równy połowie ich sumę.

Teraz rozważmy podstawowe wzory, które definiują kształty geometryczne. Aby to zrobić, należy założyć, że A i B – podstawa; C (prostopadłe do dna) i D – boki prostokątnego trapezu, M – środkową linię, a – kąt ostry, P – obszar.

1. prostopadły do podstawy, Figura równej wysokości (C = N) i jest równa długości drugiej strony A i sinusa kąta w większej podstawy (C = * sinα). Co więcej, jest równy iloczynowi tangensa kąta ostrego a różnica w bazach: C = (A-B) * tgα.

2. Po stronie D (prostopadłe do dna) jest równa ilorazowi różnicy A i B oraz cosinus (a) albo kątem ostrym do wysokości prywatnej figury H oraz sinus kąta ostrego: A = (A-B) / cos α = C / sinα.

3 po stronie, która jest prostopadła do podstawy, jest równa pierwiastkowi kwadratowemu z kwadratu różnicy D – drugi bok – i kwadratową różnice bazowe:

C = √ (Q2 (A-B), 2).

4. Boczne prostokątny trapez wynosi pierwiastek kwadratowy z sumy kwadratu strony i C zasad różnica geometryczny kształt: d = √ (C2 + (A-B) 2).

5. Po stronie C jest równa ilorazowi podwójnego kwadratu sumy jego podstaw: c = P / M = 2P / (A + B).

6. Obszar określony przez produktu (M linii środkowej prostokątnego trapezu) w wysokości i kierunku poprzecznym, prostopadle do podstawy P = m * n = m * C.

7. Stanowisko C iloraz dwukrotnie kwadratowy produktem sinus kąt ostry, a suma jego podstaw: C = P / M * sinα = 2P / ((A + B) * sinα).

8. boczny wzór prostokątnego trapezu, przez jego przekątną, a kąt między nimi:

– sinα = sinβ;

– C = (* D1 D2 / (A + B)) * sinα = (* D1 D2 / (A + B)) * sinβ,

w których D1 i D2 – przekątnej trapezu; α i β – kąt między nimi.

9. Wzór z boku, pod kątem na dolnej podstawie i inni: A = (A-B) / cosα = C / sinα = h / sinα.

Ponieważ trapezowe z kątami prostymi jest szczególnym przypadkiem trapezu, inne wzory, które określają te dane, spotka i prostokątne.

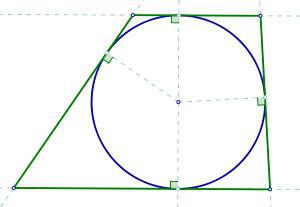
Typy trapezie

właściwości incircle

Jeśli warunek jest powiedziane, że w prostokątnym trapezowym wpisany okrąg, a następnie można użyć następujących właściwościach:

– ilość zasady wynosi suma boków;

– odległość od wierzchołka kształtu prostokątnego do punktów styczności wpisanego koła zawsze równe;

– wysokość trapezu odpowiada stronie prostopadle do podstawy, i jest równa średnicy koła ;

– koła jest punkt, w którym przecinają się dwusieczne kątów ;

– w przypadku bocznej punktu styku jest podzielona na odcinki, N i M, wtedy promień koła jest równy pierwiastkowi kwadratowemu z produktu z tych segmentów;

– czworobok utworzonej przez punkty styku, w górnej części trapezu, a środek okręgu wpisanego – to kwadrat, którego bok jest równy promieniowi;

– powierzchnia rysunku jest produktem powodu, że produkt z pół sumy zasady na jego wysokości.

podobny trapez

Ten temat jest bardzo przydatna do badania własności figur geometrycznych. Na przykład, przekątną podzielony na cztery trójkąty trapezowy i przylega do podstawy, jak i na boki – równe. To stwierdzenie można nazwać własnością trójkątów, który jest zepsuty trapez jego przekątne. Pierwsza część tego oświadczenia jest udowodnione przez znak podobieństwa dwóch rogach. Aby udowodnić, druga część jest lepiej zastosować metodę opisaną poniżej.

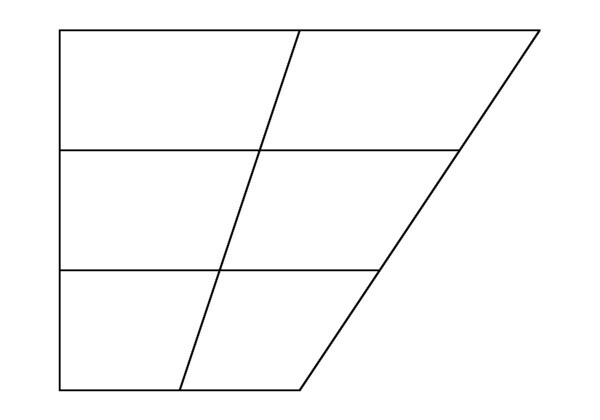
jak trapez

dowód

Przyjąć, że ABSD rysunku (AD i BC – podstawa trapezu) jest podzielona przekątnych AC i HP. Punkt przecięcia – O. Otrzymujemy cztery trójkąty AOC – Na dolnej podstawy, BOS – górnej podstawy, ABO i SOD po bokach. Trójkąty SOD i biofeedback mają wspólną wysokość w takim przypadku, jeśli odcinki BO i OD są ich podstawy. Uważamy, że różnica w ich obszarach (P) jest równa różnicy tych segmentach: PBOS / PSOD = BO / ml = K. konsekwencji PSOD = PBOS / K. Podobnie, trójkąty AOB i biofeedback mają wspólną wysokość. Akceptacja dla swoich segmentach bazowych SB i OA. Otrzymamy PBOS / PAOB = CO / OA = K PAOB = PBOS / K. Z tego wynika, że PSOD = PAOB.

Skonsolidować materialne studenci są zachęcani, aby znaleźć połączenie między obszarami trójkątów otrzymanych, który jest zepsuty trapez jego przekątne, decydując następnego zadania. Wiadomym jest, że trójkąty BOS i ADP obszary są równe, konieczne jest, aby znaleźć obszar trapezu. Od PSOD = PAOB, następnie PABSD PBOS + = PAOD 2 * PSOD. Z podobieństwa trójkątów BOS i ANM wynika, że BO / OD = √ (PBOS / PAOD). W związku z tym, PBOS / PSOD = Bo / OD = √ (PBOS / PAOD). Uzyskaj PSOD = √ (* PBOS PAOD). Następnie PABSD PBOS + = PAOD 2 * √ (PAOD PBOS *) = (+ √PBOS √PAOD) 2.

właściwości podobieństwo

Kontynuując rozwijać tego tematu, jest to możliwe do udowodnienia, a inne interesujące cechy trapezów. Tak więc, za pomocą podobieństwa może okazać segment właściwość, która przechodzi przez punkt utworzonej przez przecięcie przekątnych geometrycznej, równolegle do ziemi. Do tego rozwiązać następujący problem: trzeba znaleźć segment RK długości, która przechodzi przez punkt O. z podobieństwa trójkątów ADP i SPU wynika, że AO / OS = AD / BS. Z podobieństwa trójkątów ADP i ASB wynika, że AB / AC = PO / AD = BS / (BP + BS). Oznacza to, że BS * PO = AD / (AD + BC). Podobnie, z podobieństwa trójkątów MLC i ABR wynika, że OK * BP = BS / (BP + BS). Oznacza to, że OC i RC = RC = 2 * BS * AD / (AD + BC). Segment przechodzącą przez punkt przecięcia przekątnych równolegle do podstawy i połączenie dwóch boków, punkt przecięcia jest podzielony na pół. Jego długość – jest średnią harmoniczną liczb powodu.

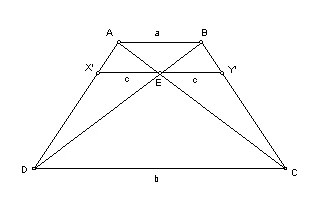
Rozważmy następujące cechy trapezu, który nazywany jest własnością czterech punktów. punktem przecięcia przekątnych (D), przy czym punkt przecięcia utrzymania boków (E), jak również połowy zasad (T i G) zawsze znajdują się na tej samej linii. Jest to łatwe do udowodnienia sposób podobieństwo. Powstałe trójkąty są podobne i BES AED i każda zawiera medianę ET i DLY podziału kąt wierzchołkowy E w równych częściach. W związku z tym, punkt E, T i K są współliniowe. Podobnie, w jednej linii umieszczone są w przeliczeniu na T, O i G. Wynika to z podobieństwa trójkątów BOS i ANM. Stąd wnioskujemy, że wszystkie cztery warunki – E, T, O i F – będzie leżą na linii prostej.

Stosując podobne trapezy, mogą być oferowane studentom znaleźć długość segmentu (LF), który dzieli się na dwie postać podobnego. To cięcie musi być równoległa do podstawy. Od otrzymanej trapezu ALFD LBSF i podobne, BS / LF = LF / AD. Oznacza to, że LF = √ (BS * BP). Wnioskujemy, że segment dzieli się na dwa trapezu podobnego, ma długość równą średniej geometrycznej długości podstaw postać.

Rozważmy następującą właściwość podobieństwa. Jest on oparty na segmencie, który dzieli trapez na dwie równe kawałki wielkości. Przyjąć, że odcinek trapezowy ABSD jest podzielony na dwa podobne EH. Ze szczytu B obniżona wysokość tego segmentu jest podzielony na dwie części En – B1 i B2. Uzyskanie PABSD / 2 = (BS + EH) * V1 / 2 = (AP + EH) * B2 / 2 = PABSD (BP + BS) * (B1 + B2) / 2. Dalsze składających się na system, w którym pierwszy wzór (PN + EH) B1 * = (BP + EH) * B2 i drugi (PN + EH) B1 * = (BP + Bs) * (b1 + b2) / 2. Wynika stąd, że B2 / B1 = (BS + EH) / (BP + EH) i BS + EH = ((BS + BP) / 2) * (1 + B2 / B1). Okazuje się, że długość podzielenie na dwie równe trapezowego, odpowiadającą średniej długości podstawy kwadratowa: √ ((CN2 + ÅQ2) / 2).

wnioski podobieństwo

W ten sposób udowodniliśmy, że:

1. Segment łączący środek trapezu na bocznych stronach, równolegle do BP i BS oraz BS jest średnią arytmetyczną i (długość podstawy trapezu) pz.

2. Pasek przechodzącej przez punkt O przecięcia przekątnych równolegle AD i bc jest równa średniej harmonicznej numerów BP BS (2 x BS * ne / (AD + BC)).

3. Segment zerwania w podobny trapezu ma długość średnia geometryczna baz BS i BP.

4. Element, który dzieli się na dwie równe kształt wielkości, długości oznaczają numery kwadratowych BP i BS.

Konsolidację materiału i świadomość powiązań pomiędzy segmentami studenta należy budować je do konkretnego trapezu. może on łatwo wyświetlania linii średniej a odcinek przechodzący przez punkt – punkt przecięcia się tych przekątnych figurach – równolegle do ziemi. Ale gdzie będzie trzecim i czwartym? Ta odpowiedź doprowadzi studenta do odkrycia nieznanej relacji między wartościami średnimi.

Odcinka łączącego punkty pośrednie przekątnych trapezu

Rozważmy następującą właściwość figury. Przyjąć, że MN segment jest równoległa do podstawy, dzieląc na pół po przekątnej. punkt przecięcia jest nazywany W S. Segment ten jest równy połowie powodu różnicy. Zbadajmy to bardziej szczegółowo. MSH – średnia linia trójkąta ABS jest równy BS / 2. Minigap – środkową linię DBA trójkąta jest równa AD / 2. Potem okazuje się, że SHSCH = minigap-MSH dlatego SHSCH = AD / 2-BS / 2 = (AD + BC) / 2.

Środek ciężkości

Spójrzmy na sposób definiowania elementu dla danej figury geometrycznej. Aby to zrobić, należy rozszerzyć bazę w przeciwnych kierunkach. Co to znaczy? Jest to konieczne, aby dodać podstawy do górnej dołu – do którejkolwiek ze stron, na przykład, w prawo. Niższa przedłużenie długości górnym rogu. Następnie połączyć ich przekątnej. Punkt przecięcia tego segmentu z linią środkową na rysunku jest środkiem ciężkości trapezu.

Wpisane i opisane trapez

Lista niech dysponuje takie dane:

1. Linia może być wpisany w okrąg tylko wtedy, gdy jest równoramienny.

2. Wokół koła można określić jako trapezu, pod warunkiem, że suma długości ich podstaw jest sumą długości boków.

Konsekwencje wpisanego koła:

1. Wysokość trapezu opisana zawsze równy dwukrotności promienia.

2. boku trapezu opisane jest, patrząc od środka koła pod kątem prostym.

Pierwszą konsekwencją jest oczywista, i udowodnić, drugi jest zobowiązany do wykazania, że kąt SOD jest bezpośredni, czyli w rzeczywistości, również nie będzie łatwe. Ale wiedza o tej właściwości pozwala na korzystanie trójkąt prostokątny, aby rozwiązać problemy.

Teraz musimy określić konsekwencje dla trapezu równoramiennego, który jest wpisany w okrąg. Otrzymamy że wysokość jest średnia geometryczna postać podstawy H = 2 ^ = √ (BS * BP). Spełniając podstawowe metody rozwiązywania problemów dla trapezów (zasada dwóch wysokościach), student musi rozwiązać następujące zadanie. Przyjąć, że BT – wysokość figurki ABSD równoramienny. Trzeba znaleźć odcinki AT i AP. Stosując wzór opisany powyżej, to nie jest trudne.

Teraz nam wyjaśnić jak określić promień okręgu z obszaru określonego trapezu. Pominięte w górnej wysokości B na bazie BP. Ponieważ koło wpisane w kształcie trapezu, BS + 2AB = BP lub AB = (PN + BP) / 2. Z trójkąta ABN find sinα = BN / 2 * AB = BN / (AD + BC). PABSD = (bs + BP) BN * / 2 BN = 2P. Uzyskanie PABSD = (BP + BS) * R wynika, że R = PABSD / (AD + BC).

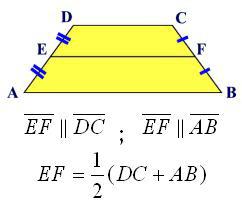
, co jest w środku linii trapezu