Prawdziwe liczby i ich właściwości

Pythagoras twierdził, że liczba ta leży u podstawy świata na równi z głównymi elementami. Platon wierzył, że liczba ta łączy zjawisko i noumenon, pomagając poznawać, mierzyć i wyciągać wnioski. Arytmetyka pochodzi od słowa "arithmos" – liczby, początek rozpoczął się w matematyce. Nim potrafi opisać każdy przedmiot – od podstawowego jabłka po abstrakcyjne przestrzenie.

Potrzeby jako czynnik rozwoju

Na początkowych etapach kształtowania się społeczeństwa potrzeby ludzi ograniczały się do konieczności zachowania punktacji – jednego worka zboża, dwóch worków zbożowych itp. Aby to zrobić wystarczy mieć naturalne liczby, których zestaw jest nieskończoną liczbą całkowitą dodatnią N.

Później, wraz z rozwojem matematyki jako nauką, powstała potrzeba oddzielnego pola liczb całkowitych Z – zawiera ujemne ilości i zero. Jego wygląd na poziomie gospodarstw domowych sprowokowany był faktem, że w dziale księgowości podstawowej konieczne było jakoś naprawienie długów i strat. Na poziomie naukowym ujemne liczby umożliwiły rozwiązanie najprostszych równań liniowych. Między innymi okazało się, że pojawił się trywialny układ współrzędnych, ponieważ pojawił się punkt odniesienia.

Kolejnym krokiem było wprowadzenie liczb ułamkowych, ponieważ nauka nie stała w miejscu, coraz więcej nowych odkryć wymagało teoretycznej podstawy nowego impulsu wzrostu. Więc pojawiło się pole racjonalnych liczb Q.

Wreszcie racjonalność przestała odpowiadać na wnioski, ponieważ wszystkie nowe wnioski wymagały uzasadnienia. Pojawiło się pole liczb rzeczywistych, prace Euklides'a dotyczące niewspółmierności pewnych ilości ze względu na ich irracjonalność. Oznacza to, że starożytni greccy matematycy umieścili tę liczbę nie tylko jako stałą, ale również jako wartość abstrakcyjną, która charakteryzuje się stosunkiem niewymiennych ilości. Ze względu na fakt, że pojawiły się prawdziwe liczby, "wartości", takie jak "pi" i "e", "widzieli światło", bez których nowoczesna matematyka nie mogła mieć miejsca.

Ostateczną innowacją była złożona liczba C. Odpowiadała na liczne pytania i nie zgadzała się z wprowadzonymi wcześniej postulatami. Ze względu na szybki rozwój algebry, wynik był przewidywalny – posiadanie prawdziwych liczb, rozwiązanie wielu problemów było niemożliwe. Na przykład, ze względu na złożone liczby, wyszczególniono teorie ciągów i chaosów, poszerzono równania hydrodynamiki.

Teoria zbiorów. Cantor

Koncepcja nieskończoności przez cały czas była kontrowersyjna, ponieważ nie można jej było udowodnić, ani nie obaliła. W kontekście matematyki, która działała ściśle zweryfikowanymi postulatami, to najwyraźniej manifestowało się to wyraźnie, zwłaszcza że aspekt teologiczny wciąż miał wagę w nauce.

Jednakże, dzięki pracy matematyka Georga Cantora, wszystko upłynęło wraz z upływem czasu. Udowodnił, że nieskończone zestawy istnieją nieskończony zestaw i że pole R jest większe niż pole N, niech obie nie mają końca. W połowie XIX wieku jego idee były głośno nazywane "delirium" i przestępstwem przeciwko klasycznym, niezmiennym kanonom, ale czas na wszystko.

Podstawowe właściwości pola R

Prawdziwe liczby mają nie tylko takie same właściwości jak pod-misje, które są w nich zawarte, ale są uzupełniane innymi przez wagę ich elementów:

• Zero istnieje i należy do pola R. c + 0 = c dla dowolnego c w R.
• Zerowe istnieje i należy do pola R. c x 0 = 0 dla dowolnego c w R.
• Stosunek c: d dla d ≠ 0 istnieje i jest prawdziwy dla dowolnego c, d w R.
• Pole R jest uporządkowane, tzn. Jeśli c ≤ d, d ≤ c, to c = d dla dowolnego c, d w R.
• Dodanie w polu R jest przemienne, tzn. C + d = d + c dla dowolnego c, d w R.
• Mnożenie w polu R jest przemienne, tzn. Cx d = dx c dla dowolnego c, d w R.
• Dodanie w polu R jest skojarzone, tj. (C + d) + f = c + (d + f) dla dowolnego c, d, f w R.
• Mnożenie w polu R jest asocjacyjne, to jest (c x d) x f = c x (d x f) dla dowolnego c, d, f w R.
• Dla każdego numeru z pola R istnieje odwrotność, tak że c + (-c) = 0, gdzie c, -c od R.
• Dla każdej liczby w polu R istnieje odwrotna taka, że c c c c = 1, gdzie c, c ^-1 z R.
• Jednostka istnieje i należy do R, tak że c x 1 = c, dla dowolnej c w R.
• Prawo dystrybucyjne posiada tak, że c (d + f) = c x d + c f f dla dowolnego c, d, f w R.
• W polu R zero nie jest równe.
• Pole R jest przejściowe: jeśli c ≤ d, d ≤ f, to c ≤ f dla dowolnego c, d, f w R.
• W polu R kolejność i dodatki są ze sobą powiązane: jeśli c ≤ d, to c + f ≤ d + f dla dowolnych c, d, f w R.
• W polu R porządek i mnożenie są ze sobą powiązane: jeśli 0 ≤ c, 0 ≤ d, to 0 ≤ c x d dla dowolnego c, d z R.
• Zarówno ujemna, jak i dodatnia liczba rzeczywista są ciągłe, tzn. Dla dowolnego c, d w R istnieje f z R, tak że c ≤ f ≤ d.

Moduł w polu R

Prawdziwymi liczbami są takie rzeczy jak moduł. 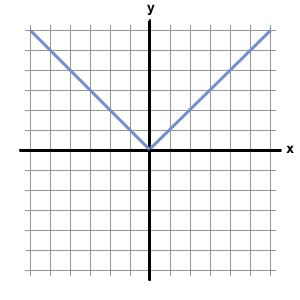Oznacza się jako | f | Dla dowolnego f w R. | f | = F, jeśli 0 ≤ f i | f | = -f if 0> f. Jeśli weźmiemy pod uwagę moduł jako wartość geometryczną, oznacza to przebyty dystans – nie ma znaczenia, czy "przechodzisz" przez zero w punkcie minus lub przechodzisz do plusa.

Złożone i prawdziwe liczby. Co jest powszechne i jakie są różnice?

Ogólnie rzecz biorąc, liczby złożone i rzeczywiste są takie same, za wyjątkiem tego, że jednostka imaginacyjna i, której kwadrat wynosi -1, dołączyła do pierwszego. Elementy pól R i C można przedstawić następująco:

• C = d + fx i, gdzie d, f należy do pola R, a i jest jednostką wyimaginowaną.

Aby uzyskać c od R w tym przypadku, f jest po prostu uważane za równe zeru, to jest tylko część rzeczywista liczby. Ponieważ pole liczb zespolonych ma ten sam zestaw właściwości co pole liczb rzeczywistych, f xi = 0, jeśli f = 0.

Jeśli chodzi o różnice praktyczne, na przykład w polu R równanie kwadratowe nie jest rozwiązane, jeśli dyskryminator jest ujemny, podczas gdy pole C nie narzuca takiego ograniczenia ze względu na wprowadzenie jednostki wyobrażalnej i.

Wyniki

"Cegły" aksjomatów i postulatów, na których opiera się matematyka, nie zmieniają się. Niektóre z nich, w związku ze wzrostem informacji i wprowadzeniem nowych teorii, umieszczają następujące "cegły", które w przyszłości mogą stać się podstawą dla następnego etapu. Na przykład liczba naturalna, mimo że jest podzbiorem prawdziwego pola R, nie traci znaczenia. Na nich jest podstawowa arytmetyka, z którą zaczyna się rozpoznawanie człowieka na świecie.

Z praktycznego punktu widzenia prawdziwe liczby wyglądają jak linia prosta. Na nim można wybrać kierunek, wskazać początek i krok. Linia składa się z nieskończonej liczby punktów, z których każda odpowiada jednemu prawdziwemu numerowi, racjonalnego czy nie. Z opisu jasno wynika, że mówimy o koncepcji budowania zarówno matematyki w ogóle, jak i analizy matematycznej .