Binary Search – jeden z najprostszych sposobów, aby znaleźć element w tablicy
Dość często, programiści, nawet początkujący, w obliczu faktu, że istnieje zbiór liczb, które muszą znaleźć konkretny numer. Jest to kolekcja nazywa się tablicą. I znaleźć w nim przedmiotów, istnieje mnóstwo sposobów. Ale najprostszym z nich można uznać za binarnego wyszukiwania po prawej stronie. Jaka jest ta metoda? I jak wdrożyć przeszukiwanie binarne? Pascal jest najprostszym środowisko za organizację takiego programu, więc użyjemy go do studiowania.
Po pierwsze, przeanalizować, jakie są zalety tej metody, to jest tak, możemy zrozumieć,  jaki jest sens w studium tematu. Więc, niech mają tablicę o wymiarze co najmniej 100000000 elementów, które muszą znaleźć jakiś. Oczywiście, ten problem można łatwo rozwiązać za pomocą prostego wyszukiwania liniowego, w którym używamy cyklu porówna wymaganego elementu z tych wszystkich, które są w tablicy. Problemem jest to, że realizacja tego pomysłu zajmie zbyt dużo czasu. W prostym Pascal programu do kilku zabiegów i trzech linii tekstu głównego, nie zauważy, ale kiedy dochodzimy do bardziej lub mniej dużych projektów z dużą liczbą oddziałów i dobrej funkcjonalności, program będzie gotowy do załadowania na zbyt długo. Zwłaszcza wtedy, gdy komputer jest słaba wydajność. Dlatego też nie jest binarny wyszukiwania, co zmniejsza czas wyszukiwania przynajmniej dwukrotnie.
jaki jest sens w studium tematu. Więc, niech mają tablicę o wymiarze co najmniej 100000000 elementów, które muszą znaleźć jakiś. Oczywiście, ten problem można łatwo rozwiązać za pomocą prostego wyszukiwania liniowego, w którym używamy cyklu porówna wymaganego elementu z tych wszystkich, które są w tablicy. Problemem jest to, że realizacja tego pomysłu zajmie zbyt dużo czasu. W prostym Pascal programu do kilku zabiegów i trzech linii tekstu głównego, nie zauważy, ale kiedy dochodzimy do bardziej lub mniej dużych projektów z dużą liczbą oddziałów i dobrej funkcjonalności, program będzie gotowy do załadowania na zbyt długo. Zwłaszcza wtedy, gdy komputer jest słaba wydajność. Dlatego też nie jest binarny wyszukiwania, co zmniejsza czas wyszukiwania przynajmniej dwukrotnie.
Więc, jaka jest zasada działania tej metody? Natychmiast należy powiedzieć, że przeszukiwanie binarne pracuje nie jest w żaden tablicy, ale tylko na posortowanej zbioru liczb. Na każdym krokiem środkowy element macierzy (to znaczy numer tego elementu). Jeżeli wymagana liczba jest większa od średniej, to wszystko, co pozostało, to jest mniej niż średnia komórki, może być odrzucone, a nie tam szukać. I odwrotnie, jeśli mniej niż przeciętnie – wśród tych liczb po prawej stronie, nie można wyszukać. Następnie wybierz nowy obszar wyszukiwania, gdzie pierwszym elementem będzie środkowy element całej tablicy, a ostatnia i ostatnia wola. Średnia ilość nowe pole będzie ź wszystkich segmentów, czyli (+ ostatniego elementu środkowego elementu całej tablicy) / 2. Ponownie, te same operacje przeprowadza się – w stosunku do średniej liczby tablicy. Jeśli wartość docelowa jest niższa niż średnia, odrzucamy prawą stronę, a także robić dalej, aż do teraz ten środkowy element nie byłoby pożądane.
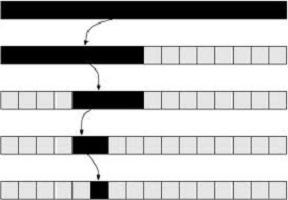
Oczywiście, najlepiej jest spojrzeć na przykład, jak napisać przeszukiwanie binarne. Pascal tutaj będzie pasować do każdego – wersja nie jest ważne. Napiszmy prosty program.
Jest to tablica 1 H pod nazwą „Massiv” zmienną wskazującą dolną granicę wyszukiwania, zwany „niz”, górna granica, zwany „Verh” średnia wyszukiwania Określenie – „sredn”; a wymagana liczba – „ISK”.
Więc, po pierwsze możemy przypisać górną i dolną granicę zakresu wyszukiwania:
niz: = 1;
Verh: = h + 1;
Następnie zorganizować cykl „aż dno jest poniżej górnej granicy”:
Choć niz <Verh – 1 zrobić
rozpocząć
Na każdym kroku, dzielimy segment 2:
sredn: = (niz + Verh) Gr 2; {Pomocą div funkcji, gdyż podziału bez reszty}
Każdy czas przeglądu. Ponieważ pozycja została już znaleźć, jeśli pożądane jest medium, przerwać cykl:
іf sredn = isk czym przerwy;
Jeżeli środkowy element tablicy bardziej niż jest to pożądane, usunięty z lewej strony, to jest górna granica średniej wyznacza Element:
Jeśli Massiv [sredn]> isk następnie Verh: = sredn;
A jeśli wręcz przeciwnie, sprawia, że dolna granica:
inny niz: = sredn;
kończyć;
To wszystko, co będzie w programie.
Zastanówmy się, jak będzie wyglądać metody binarnej w praktyce. Rozważmy następujący układ: 1, 3, 5, 7, 10, 12, 18 i prosi o numerze 12.
W sumie mamy 7 elementów, więc czwartą średniej, wartość 7.
| 1 | 3 | 5 | 7 | 10 | 12 | 18 |
Od ponad 12, 7, 1,3 i 5 elementów, możemy odrzucić. Potem mamy numer 4, 4/2 nie pozostałość 2. Tak, nowy element będzie średnio 10.
| 7 | 10 | 12 | 18 |
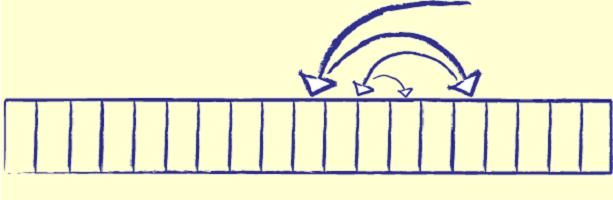 Od 12 jest większa niż 10, możemy odrzucić 7. pozostaje tylko 10, 12 i 18.
Od 12 jest większa niż 10, możemy odrzucić 7. pozostaje tylko 10, 12 i 18.
Tutaj, element środkowy jest już 12, to wymagana liczba. To zadanie jest zakończona – numer 12 uważało.