Różnice – co to jest? Jak znaleźć różnicę funkcji?

Wraz z pochodnymi ich funkcje Różnice – to niektórych podstawowych pojęć na rachunek różnicowy, w sekcji analizy matematycznej. Jako nierozerwalnie związane, oba z nich kilka wieków powszechnie stosowany w rozwiązywaniu niemal wszystkie problemy, które powstały w ramach działalności naukowej i technicznej.

Pojawienie się koncepcji dyferencjału

Po raz pierwszy stało się jasne, że taki mechanizm różnicowy, jeden z założycieli (wraz z Isaakom Nyutonom) Rachunek różniczkowy słynnego niemieckiego matematyka Gotfrid Vilgelm Leybnits. Przed, że matematycy 17 wieku. używany bardzo niejasne i mgliste pojęcie o jakiejś nieskończenie „niepodzielny” jakiejkolwiek znanej funkcji, co stanowi bardzo małą stałą wartość, ale nie jest równa zeru, poniżej której wartościami funkcja nie może być po prostu. W związku z tym, że tylko jeden etap wprowadzenia pojęć nieskończenie małych odstępach argumentów funkcji i ich przyrosty funkcji, które mogą być wyrażone w pochodnych tego ostatniego. I ten krok został podjęty niemal równocześnie powyższe dwóch wielkich naukowców.

Opierając się na potrzebę podjęcia pilnych praktycznych mechaniki problemów, które stoją przed nauka rozwija się bardzo szybko przemysłu i techniki, Newton i Leibniz tworzone wspólne sposoby znalezienia funkcji szybkości zmian (zwłaszcza w odniesieniu do mechanicznego prędkości ciała znanej trajektorii), co doprowadziło do wprowadzenia takich pojęć, jako funkcja pochodna, a różnica, a także okazało się, że algorytm odwrotny rozwiązania problemu, ponieważ znane per se (zmienna) prędkości przepływa znaleźć ścieżki, które doprowadziły do koncepcji integralną Ala.

W pracach Leibniza i Newtona za pomysł pierwszy okazało się, że różnice – jest proporcjonalna do przyrostu podstawowych argumentów Ah przyrosty funkcji AU, które mogą być z powodzeniem stosowane do obliczania wartości tego ostatniego. Innymi słowy, odkryli, że funkcja przyrost może znajdować się w dowolnym punkcie (w swojej domenie definicji) wyraża się jej pochodna zarówno AU = y „(x) AH + αΔh gdzie α AH – pozostałą, dąży do zera, gdy AH → 0, dużo szybciej niż rzeczywisty AH.

Według twórców analizy matematycznej, mechanizmy różnicowe – to jest dokładnie to pierwszy termin w przyrostach żadnej funkcji. Nawet bez wyraźnie zdefiniowane sekwencje granica pojęcie rozumie intuicyjnie, że wartość różnicy pochodnej zwykle działa przy Ah → 0 – AU / Ah → y „(x).

W przeciwieństwie do Newtona, który był głównie fizykiem i aparat matematyczny traktować jako narzędzie pomocnicze do badania problemów fizycznych, Leibniz zwrócić większą uwagę na ten zestaw narzędzi, w tym system wizualnych i zrozumiałymi symbolami wartości matematyczne. To on proponowany standardowego zapisu funkcji różnice dy = y „(x) dx dx i pochodnej funkcji argumentu ich stosunki y” (x) = dy / dx.

Nowoczesna definicja

Jaka jest różnica w zakresie nowoczesnej matematyki? Jest to ściśle związane z pojęciem zmiennej przyrostu. Jeśli zmienna y przyjmuje pierwszą wartość Y Y = _1, a Y = Y _2, Y różnicy ₂ ─ R ₁ jest nazywany wartością przyrostu Y. 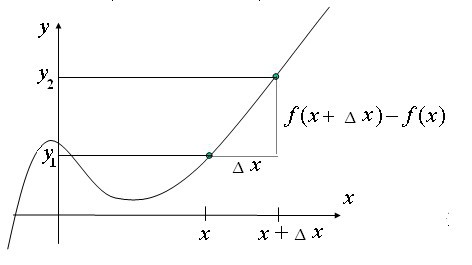Przyrost może być pozytywna. ujemne i zero. Słowo „przyrost” oznaczono §, AU zapisu (odczyt „y delta”) oznacza wartość przyrostu y. tak AU = _y2 ─ _y1.

Jeżeli wartość AU dowolną funkcją y = f (x) może być przedstawiony jako AU = A AH + a, gdzie A oznacza brak zależności od DH, t. E. = const dla współrzędnych X i α terminowi Ah → 0 tendencję do jest to jeszcze szybciej niż rzeczywisty Ah, po czym pierwszy ( „master”) okres proporcjonalny AH i jest y = f (x) Różnica oznaczoną DY i DF (x) (odczyt "y de", "De eff od X"). Dlatego różnicowego – „główną” liniowe w odniesieniu do składników przyrostów funkcji AH.

mechaniczne wyjaśnienie

Niech s = f (t), – odległość w linii prostej ruchomym punktem materiału z położenia początkowego (t – czas podróży). Przyrost Δs – oznacza punkt sposób podczas przedziału czasowego At, a DS różnicowe = F „(t) At – takie rozwiązanie, które wskazują, że jest przeznaczone do tego samego czasu AT, jeżeli zachowana prędkości f” (t), osiągnięta w chwili t , Gdy nieskończenie At DS urojony ścieżka różni się od rzeczywistego Δs nieskończenie o wyższego rzędu w stosunku do At. Jeśli prędkość w chwili t jest równa zeru, to wartości DS przybliżeniu daje niewielki punkt odchylenia.

interpretacja geometryczna

Niech linia L jest wykresem y = f (x). Następnie Δ X = MQ AU = QM „(patrz fig. Poniżej). Styczna MN łamie AU pokroić na dwie części, QN i NM”. Pierwszy i Dh jest proporcjonalna QN = MQ ∙ Tg (QMN kąt) = AHf „(x), t. E Qn dy różnicowego.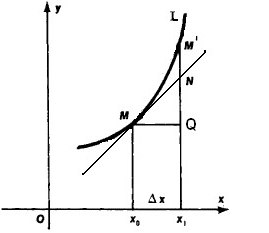

Druga część różnicy AU NM'daet ─ dy, gdy Ah Długość → 0 NM „spada jeszcze szybciej niż przyrost argumentu, to znaczy ma kolejność małości wyższej niż AH. W tym przypadku, jeśli F „(x) ≠ 0 (nierównoległe stycznych OX) segmentów odpowiadających QM'i QN; Innymi słowy NM „gwałtownie maleje (kolejność małości na wyższy) niż całkowity przyrost AU = QM”. Jest to widoczne na rysunku (zbliża pierścień M'k M NM'sostavlyaet wszystkim mniejszy odsetek QM „segment).

Tak graficznie dowolną funkcją różnicy jest równa przyrostu rzędnej stycznej.

Pochodną i różnica

Czynnikiem, w pierwszym okresie funkcji skokowej ekspresja jest równa wartości jego pochodne „f (x). Tak więc, następujący związek – D = F '(x) df Dh lub (x) = F' (x) Ah.

Wiadomo, że przyrost niezależnego argumentu równa jest różnicy AH = dx. W związku z powyższym, można napisać: F „(x) dx = dy.

Znalezienie (czasami mówi się, że „decyzja”) różnicowych jest wykonywana przez tych samych zasadach jak w przypadku pochodnych. Lista z nich znajduje się poniżej.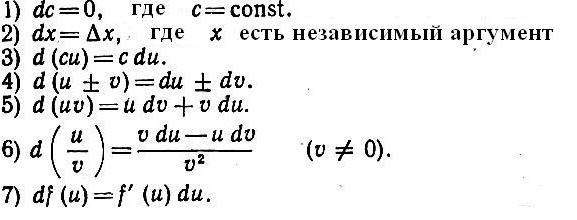

Co jest bardziej uniwersalny: przyrost argumentu lub jego dyferencjału

Tutaj trzeba dokonać pewnych wyjaśnień. Reprezentacja wartości F „(x), różnica Ah możliwe rozważając X jako argument. Jednak funkcja może być złożona, w którym x może być funkcją argumentu t. Następnie przedstawieniem ekspresji różnicowej f „(x) AH, z reguły nie jest możliwe; z wyjątkiem przypadku liniowa zależność x = w + b.

Jeśli chodzi o wzorze F „(x) dx = dy, a w przypadku niezależnego argumentu x (czym dx = AH) w przypadku parametrycznego zależność x T, to różnica.

Na przykład, wyrażenie x 2 Ah dla y = x ² różnicowaniu gdy x jest argumentem. Teraz x = t ² i zakładają t argument. To y = x ² = ^t4.

Po tym następuje (T + AT) ² = ^t2 + 2tΔt + ^At2. Stąd Dh = 2tΔt + ^At2. Stąd: 2xΔh = 2T ² (2tΔt + ^At2).

To określenie nie jest proporcjonalna do At, a więc jest 2xΔh nie różnicowego. Można go wyznaczyć z równania y = x ² = ^t4. Jest ona równa D = 4t ³ At.

Jeśli weźmiemy 2xdx ekspresyjnego, to jest różnica y = x ² na co najmniej jeden argument t. Rzeczywiście, gdy x = ^t2 uzyskania dx = 2tΔt.

Tak 2xdx = 2T ² 2tΔt = 4t ³ .DELTA.t t. E. różnice w ekspresji rejestrowane za pomocą dwóch różnych zmiennych zbieżne.

Wymiana przyrostach dyferencjały

Jeżeli F „(x) ≠ 0, AU i równoważne dy (gdy Dh → 0); Jeżeli F „(x) = 0 (czyli i dy = 0), nie są równoważne.

Na przykład, jeśli y = x ^2, po czym AU = (x + Ah) ² ─ ^X2 = 2xΔh Dh + ² i D = 2xΔh. Jeśli x = 3, to wówczas mamy AU = 6Δh + AH ² i D = 6Δh równoważne powodu Ah ² → 0, gdy x = 0, wartość AU = Ah ² i D = 0, nie są równoważne.

Fakt ten, w połączeniu z prostą budową mechanizmu różnicowego (m, E. liniowości względem DH) jest często stosowany w przybliżonym obliczenia, na założeniu, że AU ≈ dy dla małych AH. Znajdź funkcja różnica jest zwykle łatwiejsze niż obliczyć dokładną wartość przyrostu.

Na przykład, kostki mają metaliczną z krawędzią x = 10,00 cm. Podczas ogrzewania krawędzi wydłużony o DH = 0,001 cm. Jak zwiększonej objętości sześcianu V? Mamy V = ^X2, tak że dV = 3 x ² = Ah 3 ∙ ∙ ¹⁰ lutego 0/01 = 3 (cm ^3). Zwiększona AV równoważne różnica dV tak, AV = 3 ^cm3. Pełna kalkulacja dałaby ³ AV = 10,01 ─ ¹⁰ marca = 3.003001. Ale wynik wszystkich cyfr, z wyjątkiem pierwszego zawodna; Dlatego też, konieczne jest jeszcze zaokrąglić do 3 ^cm3.

Oczywiście, takie podejście jest użyteczne tylko wtedy, gdy jest to możliwe do oszacowania wartości przekazywanej z błędem.

Funkcja różnica: przykłady

Spróbujmy znaleźć różniczkę funkcji y = x ^3, znalezienie pochodnej. Dajmy przyrost argumentu AU i zdefiniowania.

AU = (Dh + X) ³ ─ x ³ = 3 x ² + H (Dh 3xΔh ² + ^3).

Tutaj, współczynnik A = 3x ² nie zależy od AH, tak, że pierwszy składnik jest proporcjonalny Ah, drugi element 3xΔh Ah ² + ³ gdy Ah → 0 maleje szybciej niż przyrost argumentu. W związku z tym, element 3x ² AH jest różnica y = x ^3:

D = 3x ² 3x Dh = ² lub d dx (x ³⁾ = 3 x ² DX.

Gdzie d (x ³⁾ / dx = 3x ^2.

Dy Teraz znaleźliśmy funkcja y = 1 / X przez pochodną. Następnie D (1 / x) / dx = ─1 / ^x2. Dlatego D = ─ Dh / ^{2 x.}

Różnicowych podstawowe funkcje algebraiczne są podane poniżej.

Szacunkowe obliczenia wykorzystujące mechanizm różnicowy

W celu oceny funkcji f (x), a jej pochodna F „(x) przy x = a często jest trudno, ale to samo w sąsiedztwie x = A nie jest łatwe. Potem przychodzi z pomocą przybliżonego wyrażenia

Rf (A + Ah) ≈ f „(A) Dh + f (a).

To daje przybliżoną wartość funkcji w małych porcjach przez różnicowaniu AHf „(a) AH.

W związku z tym wzór daje przybliżoną ekspresji dla funkcji w punkcie końcowym części długości Dh jako suma jej wartości na punkt startowy części (x = A) i różnicy w tym samym momencie początkowym. Dokładność metody określania wartości funkcji ilustruje rysunek.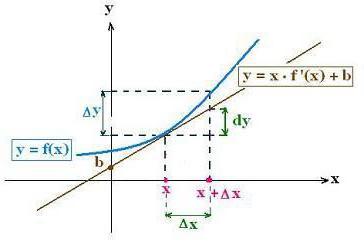

Jednakże znane i dokładny wyrażenie dla wartości funkcji X = a + AH dla wzoru skończonych skokiem (lub, alternatywnie, o wzorze Lagrange'a)

Rf (A + Ah) ≈ f „(ξ) Dh + f (a)

gdzie punkt X = a + ξ w przedziale od x = A do X = a + AH, chociaż jego dokładne położenie jest znane. Dokładna formuła pozwala ocenić błąd przybliżonego wzoru. Jeśli stawiamy w Lagrange wzorze Ę = Ah / 2, mimo że przestaje być dokładne, ale daje, z reguły o wiele lepsze podejście niż oryginalnej wypowiedzi pod względem różnicy.

wzory oceny błędu poprzez zastosowanie mechanizmu różnicowego

przyrządów pomiarowych , w zasadzie, niedokładne i doprowadzić do danych pomiarowych odpowiadających błędu. Charakteryzują się one ograniczania bezwzględnej błędu, albo w skrócie, błąd granica – dodatnia, wyraźnie przekraczającym błędu w wartości bezwzględnej (albo najwyżej równa niego). Ograniczania błędu względnego nazywa się iloraz otrzymany poprzez podział przez wartość bezwzględną wartości mierzonej.

Niech Dokładny wzór y = f (x), funkcja służąca do vychislyaeniya Y, przy czym wartość x jest wynik pomiaru, a więc powoduje błąd Y. Następnie, w celu znalezienia graniczną bezwzględny błąd │Δu│funktsii Y za pomocą wzoru

│Δu│≈│dy│ = │ F „(x) ││Δh│,

gdzie │Δh│yavlyaetsya marginalny błąd argumentem. │Δu│ ilość musi być zaokrąglona do góry w miarę niedokładne sama kalkulacja jest zastąpienie przyrostu na obliczenie różnicowego.