Powierzchnia rombu: wzory i fakty

Rombu (od greckiego i łacińskim ῥόμβος rombus «bębnie") jest równoległobokiem, który charakteryzuje się obecnością równych bokach długości. W przypadku, gdy kąty 90 stopni (albo prostopadle) tak, figura geometryczna jest nazywany kwadratowych. Romb – figura geometryczna, rodzaj czworokątów. To może być kwadratowy, a równoległobokiem.

Geneza terminu

Porozmawiajmy trochę o historii figury, które pomogą trochę odkrywa tajemnicze tajemnice starożytnego świata. Zazwyczaj słowo dla nas, często występujący w literaturze szkolnej, „diament” pochodzi od greckiego słowa „bębna”. W starożytnej Grecji, instrumenty muzyczne produkowany w kształcie rombu lub kwadratu (w przeciwieństwie do współczesnych adaptacji). Na pewno zauważyliście, że karty kombinezony – Diamonds – ma kształt rombowy. Powstawanie tego garnitur wraca do czasów, kiedy diamenty okrągłe nie są używane w życiu codziennym. W związku z tym, że diament – najstarsza postać historyczna, która została wymyślona przez człowieka na długo przed kołami.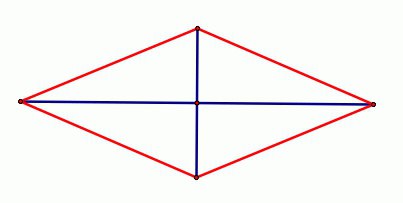

Po raz pierwszy takie słowo jak „diament” był używany przez tak znane osobistości jak Geron i Papieża Aleksandrii.

Właściwości rombu

1. Ponieważ boki romb naprzeciwko siebie i są do siebie równoległe, rombu niewątpliwie równoległobok (AB || CD AD || BC).
2. Rombowy są po przekątnej skrzyżowania pod kątem prostym (AC ⊥ BD), a więc prostopadłe. W związku z tym przecięcia dzieli na pół po przekątnej.
3. Dwusieczna rombowe romb są po przekątnej narożniki (∠DCA = ∠BCA, ∠ABD = ∠CBD i T, D).
4. Tożsamość równoległoboków, że suma kwadratów przekątnych rombu jest liczba boków kwadratu, która jest mnożona przez 4.

Znaki rombu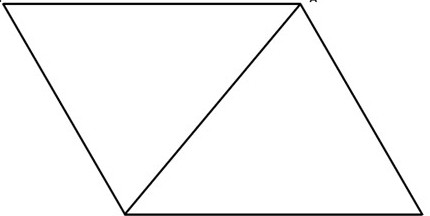

Romb w tych przypadkach jest równoległobokiem, który spełnia następujące warunki:

1. Wszystkie boki równoległoboku są równe.
2. Przekątne rombu przecinają się pod kątem prostym, to znaczy są prostopadłe względem siebie (AC⊥BD). Świadczy to o tym, że zasada z trzech stron (boki są równe i są usytuowane pod kątem 90 stopni).
3. Równoległobok przekątnej narożniki równo rozdzielone, ponieważ boki równe.

Obszar rombu

Powierzchnia rombowej może być obliczana za pomocą kilku wzorach (zależnie od materiału przewidzianego w problemu). Następnie przeczytać o tym, co jest obszar rombu.

1. Obszar rombu jest równa liczbie z których połowa jest wytworem jego przekątnych.
2. Ponieważ diament – rodzaj równoległoboku, rombu (S) jest liczbą stronie obszaru roboczego równoległoboku na jego wysokość (h).
3. Ponadto, powierzchnia rombu można obliczyć ze wzoru, który jest produktem kwadratów stronach na sinus kąta rombu. Sinus kąta – alfa – róg znajduje się pomiędzy źródłem boki rombów.
4. Dopuszczalne jest dla odpowiednich badanych roztworów wzór, który jest produktem dwukrotności kąta alfa, a promień incircle (R).

Wzory te można obliczyć i wykazać na podstawie twierdzenia Pitagorasa i zasady z trzech stron. Wiele przykładów skupiają się na zaangażowaniu kilku wzorów w jednej pracy.